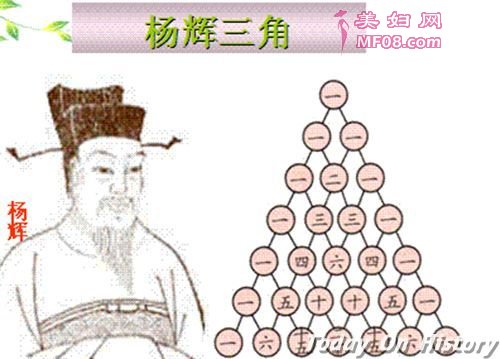
贾宪三角贾宪的数学成就

杨辉三角

　　贾宪是北宋杰出数学家，在数学、天文、历算方面都有贡献，当然，他最大的成就就是创造“贾宪三角”和“增乘开方法”，其中增乘开方法比西方早了770年。贾宪在数学上做出的贡献为算法抽象化、机械化都很有影响。

　　贾宪三角

　　“贾宪三角”又称“杨辉三角”，是二项式系数在三角形中的一种几何排列，在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现，它是是中国数学史上的一个伟大成就。

　　在中国数学史上贾宪最早发现贾宪三角形。杨辉在所著《详解九章算法》《开方作法本元》一章中作贾宪开方作法图，并说明“出释锁算书，贾宪用此术”。贾宪开方作法图就是贾宪三角形。杨辉还详细解说贾宪还发明的释锁开平方法，释锁开立方法，增乘开平方法，增乘开立方法。

　　贾宪的数学成就

　　杨辉著《详解九章算法》中曾引用贾宪的“开方作法本源”图和“增乘开方法”。而“立成释锁开方法”的给出，“勾股生变十三图”的完善，以及“增乘方求廉法”的创立，都表明贾宪对算法抽象化、程序化、机械化作出了重要贡献。

　　首先，贾宪的“增乘开方法”开创了开高次方的研究课题，后经秦九韶“正负开方术”加以完善，使高次方程求正跟的问题得以解决。加之从李冶的天元术（一元一次或高次方程）到朱世杰的四元术（四元一次或高次方程组）的建立，终于在十四世纪初建立起一套完整的方程学理论，使之成为宋元数学届最有成就的课题。

　　其次，贾宪三角的给出，开创了高阶等差级数求和问题的研究方向，朱世杰从“三角”的每条斜线上发现了“三角垜”、“撒星形垜”等高阶等差级数求和公式。

　　第三，“增乘开方法”事实上简化了筹算程序，并使程序化更加合理，这对后世筹算、捷算乃至于算具的改进是有启迪意义的。

　　第四，“细草”这一著述形式开创了一种数学研究方法，被后世数学家广为借鉴。乾嘉学派在保存和整理数学著作时，就曾对一批算书或注释或细草图说。